
Problema 1: Concurso «Retos olimpiadas » Junior (2º ESO)
Soluciones:
Hemos recibidos 14 resoluciones del problema 1 en la categoría junior, gracias por participar.
A continuación os facilitamos la solución oficial del problema 1:
Cuadrados Mágicos Multiplicativos
Si colocamos 9 números en una cuadrícula 3×3, el cuadrado que forman es mágico multiplicativo cuando el producto de los tres elementos de cualquiera de sus tres filas, sus tres columnas y sus dos diagonales es siempre el mismo.
a) Demuestra que si e es el elemento central y P el producto de cualquier línea, se verifica P = e3
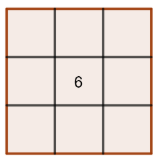
b) Completa el siguiente cuadrado mágico multiplicativo formado por nueve números enteros positivos y distintos
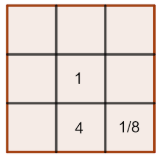
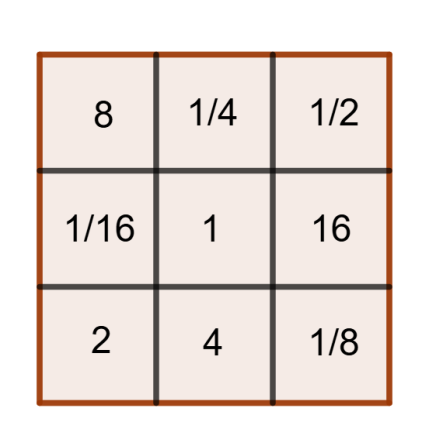
c) Completa el siguiente cuadrado mágico multiplicativo formado por nueve números racionales y distintos:
Solución oficial:
a)
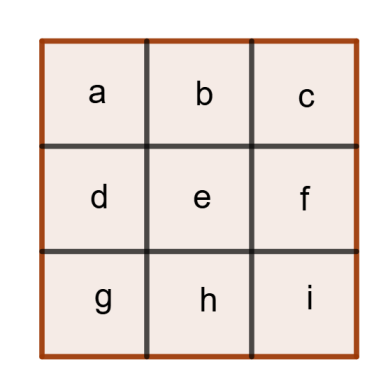
a·b·c = P; d·e·f = P; g·h·i = P; a·e·i = P; c·e·g = P
Multiplicamos la 2ª por la 4ª y por la 5ª, se obtiene: d·e·f·a·e·i·c·e·g = P3 y reagrupando:
(d·a·g)·e3·(c·f·i) = P3 pero d·a·g = P y c·f·i = P, entonces P2 . e3 = P3 de donde P = e3
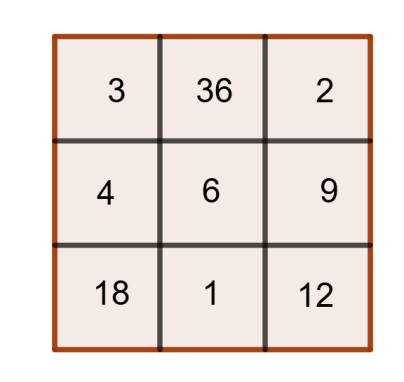
b) P = 63 = 216
Completamos una diagonal poniendo 6/2 = 3 y 6·2 = 12 y el producto de los elementos de esta diagonal es 63. La otra diagonal la completamos con 6/3 = 2 y 6·3 = 18 y también el producto es 63. Luego es muy fácil completar el cuadrado.
c) El producto de cualquier línea debe ser 1, ahora es muy fácil completar el cuadrado
Ningún alumno ha resuelto correctamente el apartado a), quizás se deba a que es una demostración con la que los alumnos de este nivel no están familiarizados. Se recomienda que vean la resolución expuesta anteriormente y que consulten con sus profesores sobre el razonamiento expuesto.
No obstante los otros dos apartados los han resuelto correctamente varios alumnos y entre ellos merecen ser mencionados Jara Matín Carbonero del IES “Norba Caesarina” de Cáceres y Nicolás Pertegal Fuentes del Colegio Nuestra Sra del Carmen de Villafranca de los Barros.
Enunciado:
8-octubre-2025
A continuación puedes ver el enunciado del problema 1 para el concurso «Retos Olimpiadas», en la categoría Junior, 2º ESO.
¡¡ Anímate a participar !! Para ello sigue las instrucciones que encontrarás tras el enunciado.
Enunciado problema 1:
Cuadrados Mágicos Multiplicativos
Si colocamos 9 números en una cuadrícula 3×3, el cuadrado que forman es mágico multiplicativo cuando el producto de los tres elementos de cualquiera de sus tres filas, sus tres columnas y sus dos diagonales es siempre el mismo.
a) Demuestra que si e es el elemento central y P el producto de cualquier línea, se verifica P = e3
b) Completa el siguiente cuadrado mágico multiplicativo formado por nueve números enteros positivos y distintos

c) Completa el siguiente cuadrado mágico multiplicativo formado por nueve números racionales y distintos:

Instrucciones para participar en el concurso:
- Descarga e imprime el documento en pdf: PROBLEMA1_JUNIOR_8_10_2025
- Realiza la resolución del problema escrito a mano en el documento impreso del punto anterior.
- Escanea en orden ascendente a la numeración de páginas los folios que hayas usado en la resolución del problema. Se guardarán en un único archivo en formato pdf (máx.10MB), nombrado problema-numero-categoría-nombre completo del participante (Ejemplo: problema2AlevinJavierSierraRosa).
- Rellena el formulario para enviar el problema. ( Se solicitan datos del alumnado pero también del representante del menor, que puede ser docente, padre, madre o tutor/a legal).
- Tienes de plazo, si quieres concursar, del 8/10/2025 al 15/10/2025. En el caso que, pasado ese período quieras enviar una resolución, puedes hacerlo, pero ya no entraría en el concurso.
RECUERDA que cuando resuelves un problema tienes que tener en cuenta los datos, anótalos si es relevante la información, realiza las operaciones en orden y explicando las que consideres importantes, y, cómo no, escribe la solución al problema planteado, contestando a la pregunta, generalmente.
Para una información más detallada, echa un vistazo a las bases: Bases del concurso «Retos Olimpiadas»
Si te surgen dudas, contacta con nosotros, te atenderemos gustosamente en Contacta con nosotros.

