1. Caja de turrones.
Uno de los productos por los que es reconocido internacionalmente Castuera es el turrón.
Con la industrialización aparecieron distintos tipos de turrón (duro, blando, de chocolate, etc) y en distintos tipos de formato (tabletas, barritas, etc).
Queremos realizar un regalo consistente en una caja con barritas de tres tipos, duro, blando y de chocolate.
Deseamos que el número de barritas del duro sean las tres quintas partes de la resta del número total de barritas de la caja menos uno, y que el número de las del blando sea la cuarta parte de la suma del número total de barritas más cuatro. También queremos que el número de barritas de chocolate sea la octava parte del total de ellas.
Realiza las siguientes cuestiones:
a) Si representamos mediante la incógnita x el número total de barritas de la caja, obtén la expresión algebraica que nos dé el número de barritas de turrón duro.
b) La expresión algebraica que nos dé el número de barritas de turrón blando.
c) La expresión algebraica que nos dé el número de barritas de turrón de chocolate.
d) Plantea una ecuación que nos permita calcular el número total de barritas de turrón.
e) Resuelve la ecuación anterior e indica el número total de barritas.
f) Calcula cuántas barritas hay de cada tipo.
2. Transformación numérica
En este año 2016 celebramos la olimpiada matemática número 25. Curiosamente puedes observar que utilizando los dígitos del año sin repetirlos y las operaciones suma, resta, multiplicación, división y potencia de exponente natural y paréntesis podemos obtener el número 25. Así por ejemplo: 20 + 6 -1 = 25.
Encuentra otras cinco expresiones numéricas cuyo valor sea 25 teniendo en cuenta las mismas condiciones.
Nota: Se considerarán iguales las expresiones que se puedan obtener una de otra mediante la propiedad conmutativa. También se considerará lo mismo +0 y -0.
3. Ventura Reyes Prósper
El matemático que da nombre a la Sociedad Extremeña de Educación Matemática nació en Castuera, sede de la fase autonómica de la primera olimpiada de matemáticas y de la próxima.
Ventura Reyes nació en el mes que menor número de letras tiene y en el día del mes que es un número primo mayor que 12 y que termina en 1, y el año en numeración romana MDCCCLXIII.
Completa la siguiente cuadrícula a partir de la información anterior y de las definiciones que se indican y escribe en el folio de soluciones el número de cada una de las cuestiones que se plantean seguida de la respuesta correspondiente:
|
1)
|
|
|
–
|
–
|
–
|
–
|
–
|
–
|
–
|
Día de nacimiento de Ventura Reyes Prósper
|
|
2)
|
|
|
|
|
–
|
–
|
–
|
–
|
–
|
Mes de nacimiento
|
|
3)
|
|
|
|
|
–
|
–
|
–
|
–
|
–
|
Año de nacimiento
|
|
4)
|
V
|
|
|
|
|
|
|
|
|
En funciones, unas son dependientes y otras independientes (en plural)
|
|
5)
|
E
|
|
|
|
|
|
|
|
–
|
Igualdad entre dos expresiones algebraicas
|
|
6)
|
N
|
|
|
|
|
|
|
|
|
Tipo de números (en plural)
|
|
7)
|
T
|
|
|
|
|
|
|
|
|
Uno de los poliedros regulares
|
|
8)
|
U
|
|
|
|
|
|
|
|
|
El que ocupa el lugar 11 (en plural)
|
|
9)
|
R
|
|
|
|
|
|
|
|
|
Cuadrilátero que es un paralelogramo(en plural)
|
|
10)
|
A
|
|
|
|
|
|
|
|
–
|
Uno de los ejes coordenados
|
4. Pancarta olímpica
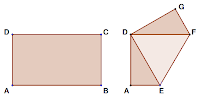
Con el fin de dar la bienvenida a la olimpiada a los alumnos participantes se ha confeccionado una pancarta rectangular. Si se pliega haciendo coincidir un vértice con el simétrico respecto al centro, se obtiene un triángulo equilátero de 2 m de lado (vértices los puntos D, E y F) tal y como se observa en la figura.
Realiza las siguientes cuestiones justificando las respuestas:
a) Calcula la altura y el área del triángulo equilátero.
b) Calcula los ángulos del triángulo de vértices los puntos D, F y G.
c) Calcula el área del pentágono de vértices los puntos A, E, F, G y D.
d) Calcula las dimensiones de la pancarta. e) Calcula el área del triángulo de vértices los puntos A, D y G.
Si quieres consultar los criterios de corrección pincha aquí.