Skip to main content
Problema1

Problemas propuestos en la Fase Comarcal de la Olimpiada Matemática 2019

Escrito por Jose Pedro en . Publicado en Olimpiada, Olimpiada 2019, Olimpiada junior.

XXVIII OLIMPIADA MATEMÁTICA EN EXTREMADURA

PROBLEMAS DE LA FASE COMARCAL

1. Burguillos del Cerro 

La edición XXVIII de la Olimpiada Matemática tendrá su sede autonómica en Burguillos del Cerro, población situada al suroeste de la provincia de Badajoz. Fue un importante asentamiento de caballeros templarios que construyeron el majestuoso castillo que corona el pueblo.

a) Deduce en qué siglo estos caballeros se asentaron en Burguillos, sabiendo que es el valor numérico del polinomio P(x)= x3 + 2x2 +13 para x = -2.

b) Calcula cuántas torres tiene el castillo, teniendo en cuenta que, si al doble le restamos la tercera parte del número aumentado en cuatro unidades, obtenemos 7.

 

2. Palabras ocultas

Problema2

A continuación mostramos diez palabras relacionadas con las matemáticas en las que se ha desordenado sus letras:

1) OTROCENRTO 2) SIVIÓNDI 3) OMAD 4) PRAECIOT 5) REFCUECNAI

6) ÓCGTNIAIN 7) RUATAL 8) SABCISA 9) OPLIONMIO 10) BLEVARIA

Indicar qué palabra representa cada una y a cuál de los siguientes bloques de contenidos matemáticos “Números y álgebra”, “Geometría”, “Funciones y gráficas” y “Estadística y probabilidad” corresponde cada una.

3. Medallón.

Problema3 1

Con motivo de la olimpiada hemos diseñado un medallón que contiene en su parte central un cuadrado de 16 cm2.

Para su construcción se ha partido de cinco cuadrados dispuestos en cruz y se han unido algunos vértices y los centros de los cuatro cuadrados exteriores tal y como se indica en las siguientes figuras.

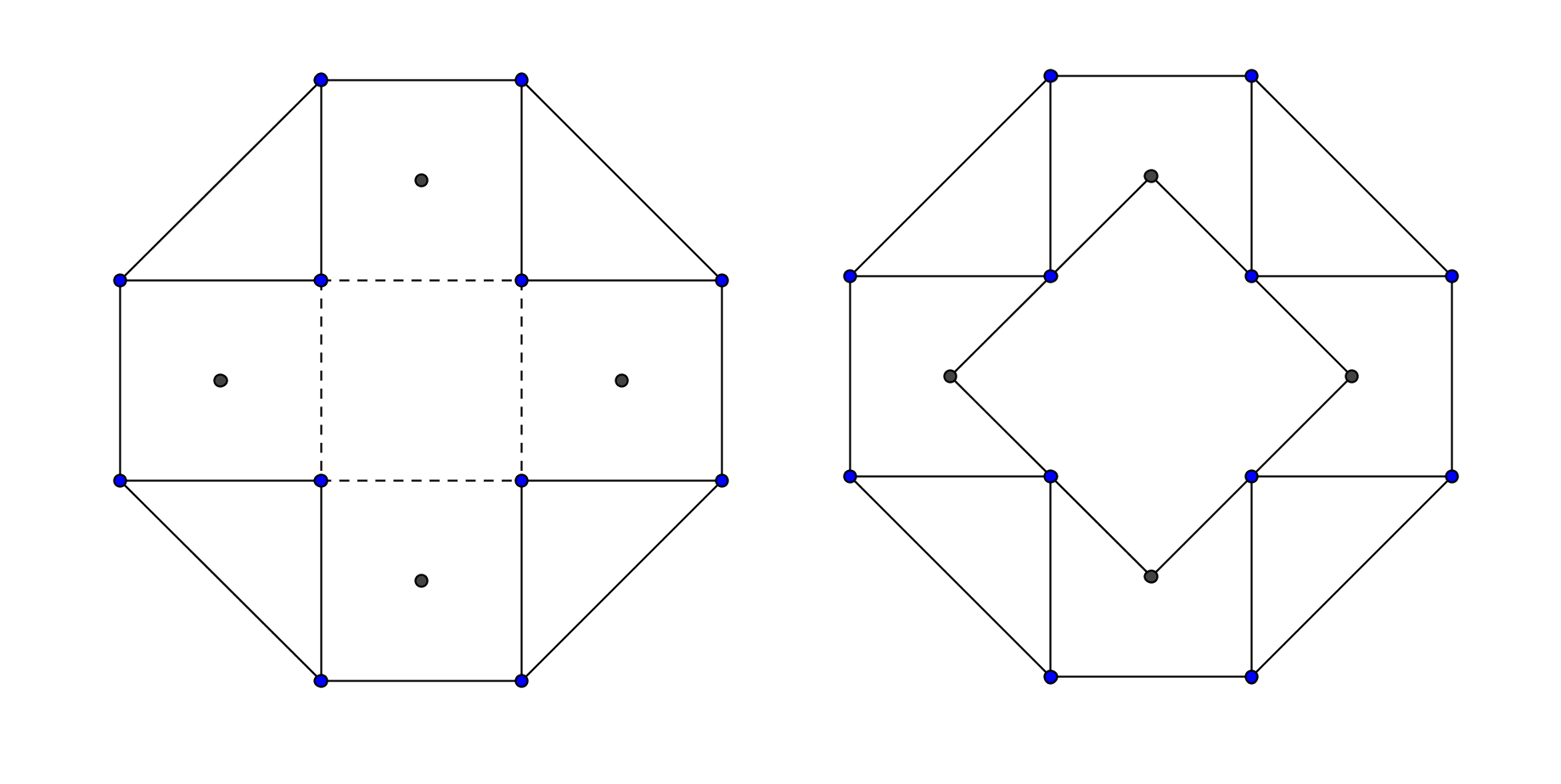Problema3 2Resuelve las siguientes cuestiones:

  1. ¿Cuánto mide el lado del cuadrado central del medallón?

  2. ¿Qué tipo de triángulos según sus lados y según sus ángulos encontramos en el medallón?

  3. ¿Cuánto mide el perímetro del medallón?

  4. ¿Qué proporción hay entre el área del cuadrado del medallón y su área total?

  5. ¿Cuántos triángulos como los que contiene el medallón se necesitan para formar un rectángulo de 40 cm de perímetro.

 

4. Caja de caudales. 

En el exterior de la caja de la figura puedes observar un código numérico escrito en numeración romana al que se le ha borrado la última letra (MMXI?) y siendo además el número completo un múltiplo de tres.

Problema4

Disponemos también de tres llaves con un código secreto cada una y queremos averiguarlos. Para ello sabemos que dichos códigos son números naturales y que cumplen las siguientes propiedades:

  1. De los códigos de la primera y segunda llave sabemos que el máximo común divisor (m.c.d.) es 11, el mínimo común múltiplo (m.c.m.) es 132 y además uno de ellos es un número primo.

  2. De la segunda y tercera llave sabemos que el m.c.d. es mayor que 11 y que el producto del m.c.d. por el m.c.m. es 34848.

Realiza las siguientes cuestiones:

  1. ¿Cuál es el código completo de la caja en notación romana y en notación decimal?

  2. ¿Cuál es el código de cada una de las tres llaves?

  3. Sabemos que la llave que abre la caja es la que cumple que la suma de los dígitos de su código es igual a la suma de los dígitos del código de la caja ¿cuál es la llave que permite abrirla?

En el siguiente enlace puedes consultar los criterios de corrección.

Criterios de corrección