Enunciados, soluciones y criterios de corrección de los problemas de la Fase regional de la XXIX Olimpiada Matemática para 2º de ESO

Problema 1: CRIPTOGRAFÍA

            La criptografía es la técnica de descifrar mensajes. Sabemos que las palabras MAS; AMO; REO y SUR se escriben encriptadas:

 

Pero NO necesariamente en ese orden.

1. Asocia cada una de estas cuatro palabras con sus correspondientes símbolos y asocia cada símbolo con una letra.
2. Descifra el siguiente mensaje:

 

 

Solución

Las palabras MAS y AMO tienen la misma letra (M), al principio y en el medio. También la segunda (A) y la primera esto nos lleva a que:

□ * ©debe ser MAS y* □ ∆  debe ser AMO

Las palabras REO y SUR tienen la misma letra (R) al principio y al final, esto nos lleva a que:

® & ∆debe ser REO y© £ ®debe ser SUR

(1 Punto por cada palabra correcta, total 4 Puntos)

La correspondencia entre símbolos y letras es:

□ = M; * = A; © = S; ∆ = O; ® = R; & = E; £ = U

(0,5 Puntos por cada símbolo correcto, total 3,5 Puntos)

Con estas correspondencias entre símbolos y letras, se tiene:

© £ □ * ® & □ ∆  © = S U M A R E M O S

(2,5 Puntos por descifrar el mensaje)

 

 

Problema 2: SEMICÍRCULO EN TRIÁNGULO

            En un triángulo rectángulo APQ de hipotenusa PQ, está inscrita una semicircunferencia de centro O y radio 12 cm. Si OP mide 15 cm, calcula la distancia OQ y el área y el perímetro del triángulo rectángulo.

 

Solución:

Al ser el radio perpendicular a cada cateto, se forma un cuadrado AROS de lado 12 cm.

PR = a  es un cateto de ORP, entonces: PR² = 15² – 12² = 81, luego PR = a = 9 cm

Los triángulos ORP y OSQ son rectángulos y semejantes, entonces:

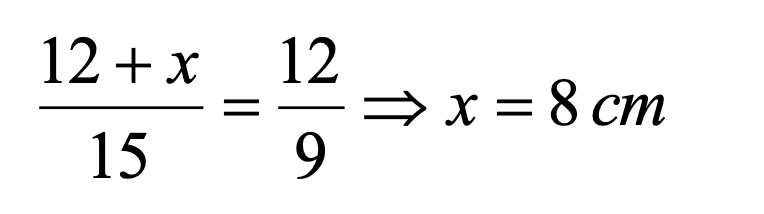
La distancia OQ es 20 cm

(5 Puntos)

En el triángulo rectángulo OSQ se tiene: b² = 20² – 12², luego b = 16 cm

El área de APQ, por ser rectángulo es:

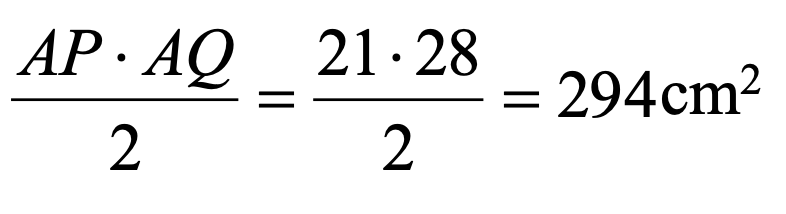
(2,5 Puntos)

El perímetro es:

35 + 21 + 28 = 84 cm

(2,5 Puntos)

 

 

Problema 3: TRABAJO EN GRUPO

            Una tarde, se reúnen en el Museo Histórico de Llerena, cinco alumnos para resolver tareas. Una de las tareas que les han propuesto es:

En una lista de siete números, si tomamos los cuatro primeros, resulta que su media es 5 y si tomamos los cuatro últimos, su media es 9. Si la media de los siete números es 7, ¿qué número ocupa la posición central?

    Visitando la Exposición de Medidas Tradicionales de Extremadura descubren una báscula antiguaa la que le faltan pesas, debido a esta circunstancia, solamente se pueden realizar pesadas de más de 60 kg. Como todos a la vez no entran en la báscula, deciden pesarse de dosen dos, con los resultados: 99, 98, 100, 103, 101, 103, 106, 102, 105, y 107 kg. ¿Cuál sería el peso de todos juntos?

Solución

 

Si llamamos a los cinco alumnos a, b, c, d y e, al pesarse de dos en dos se efectúan las siguientes pesadas; a + b; a + c; a + d; a + e; b + c;  b + d; b + e; c + d; c +e y d + e que se corresponden con las diez pesadas que se conocen pero no en qué orden.

Si sumamos las diez pesadas:

4a + 4b + 4c + 4d + 4e = 1024 de donde a + b + c + d + e = 256 kg

(5 Puntos)

 

Problema 4: ABUELOS

            A veces, cuando visito a mis abuelos, me dan una moneda de un euro o de dos euros para mis caprichos. Al volver a casa guardo la moneda en una de mis seis huchas, pero nunca mezclo monedas de diferente valor en una misma hucha.

            En el último recuento, anoté que en la primera hucha había 5 monedas, en la segunda 6, en la tercera 12, en la cuarta 14, en la quinta 23 y en la última 29.

            Ayer por la tarde gasté el contenido de una de las huchas con mis amigos. Al volver me di cuenta de que ahora tengo la mitad de monedas de un euro que de dos euros.

1. ¿Cuántas monedas he gastado?
2. ¿Cuánto dinero tengo ahorrado todavía?

Solución

1. Vamos a averiguar que hucha gastó con sus amigos.

Si después de gastar con sus amigos le quedaban “x” monedas de 1 €, de dos euros tendrá “2x” y el total de monedas que le quedaron es 3x que es múltiplo de 3.

Antes del gasto tenía: 5 + 6 + 12 + 14 + 23 + 29 = 89 monedas.

• Si gastó la hucha de 5 monedas. le quedarán 84 que es múltiplo de 3
• Si gastó la hucha de 6 monedas, le quedarán 83 que NO es múltiplo de 3
• Si gastó la hucha de 12 monedas, le quedarán 77 que NO es múltiplo de 3
• Si gastó la hucha de 14 monedas, le quedarán 75 que es múltiplo de 3
• Si gastó la hucha de 23 monedas, le quedarán 66 que es múltiplo de 3
• Si gastó la hucha de 29 monedas, le quedarán 60 que es múltiplo de 3

Las únicas huchas que pudo gastar son la de 5 monedas, la de 14, la de 23 ó la de 29 monedas.

• Si hubiese gastado la hucha de 5 monedas, le quedarían 84 monedas: 28 de 1€ y 56 de 2€ repartidas en las huchas  de: 6, 12, 14, 23 y 29 y es imposible hacer este reparto.
• Si hubiese gastado la hucha de 14 monedas, le quedarían 75 monedas: 25 de 1€ y 50 de 2€ repartidas en las huchas  de: 5, 6, 12, 23 y 29 y es imposible hacer este reparto.
• Si hubiese gastado la hucha de 23 monedas, le quedarían 66 monedas: 22 de 1€ y 44 de 2€ repartidas en las huchas  de: 5, 6, 12, 14 y 29 y es imposible hacer este reparto.
• Tuvo que gastar la hucha de 29 monedas, le quedaron 60 monedas: 20 de 1€ y 40 de 2€ repartidas en las huchas  de: 5, 6, 12, 14 y 23  y  este reparto si se puede hacer: 6 + 14 = 20 de 1€ y 5 + 12 + 23 = 40 de 2€.

Gastó 29 monedas

(3 Puntos)

1. Todavía tenía ahorradas 60 monedas, 20 de ellas en las huchas de 6 y 14 (en monedas de 1 €) y las 40 restantes en las de 5, 12 y 23 (en monedas de 2€).

El dinero que tenía ahorrado es: 20€ + 80€ = 100€

(7 Puntos)