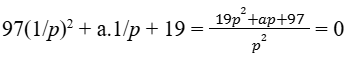Problema 5: Concurso «Retos olimpiadas » Juvenil (4º ESO)
Soluciones:
Hemos recibido nueve resoluciones del problema 5 para la categoría juvenil, ¡animaros a seguir participando!
A continuación os facilitamos la solución oficial del problema 5:
Cuerdas de Longitud Entera
El punto P dista 9 unidades del centro de una circunferencia de radio 15. ¿Cuántas cuerdas de longitud entera pasan por P? Calcula en cada caso sus longitudes
Solución oficial:
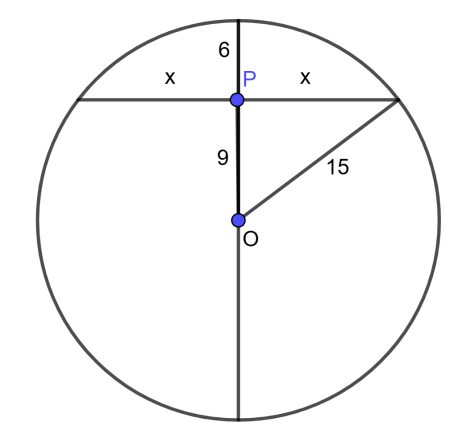
La cuerda de mayor longitud que pasa por P es el diámetro cuya longitud es 30, que es un número entero. (Una cuerda)
La cuerda de menor longitud que pasa por P es la perpendicular al diámetro, si mide 2x, se tiene: x2 = 152 – 92 = 122 de donde x = 12 y la cuerda mide 2x = 24, que es un número entero. (Una cuerda)
Al ser 24 la cuerda de menor longitud y 30 la de mayor longitud pasando por P, las cuerdas de longitud 25, 26, 27, 28 y 29 pasando por P también tienen su longitud entera y cada una de ellas hay que contarla dos veces. (Diez cuerdas). En definitiva hay 12 cuerdas que pasando por P tienen su longitud entera.
La resolución elegida como ganadora del problema 5 ha sido la realizada por Gema L. S. del IESO Sierra la Mesta (San Amalia) ¡¡ Enhorabuena !!. Merecen ser destacadas las soluciones enviadas por la alumna Victoria T. C. por su solución usando coordenadas y por la alumna Ángela S. C. por su solución usando trigonometría, ambas también del IESO Sierra la Mesta (San Amalia)



Enunciado:
3-diciembre-2025
A continuación puedes ver el enunciado del problema 5 para el concurso «Retos Olimpiadas», en la categoría Juvenil, 4º ESO.
¡¡ Anímate a participar !! Para ello sigue las instrucciones que encontrarás tras el enunciado.
Enunciado problema 5:
Cuerdas de Longitud Entera
El punto P dista 9 unidades del centro de una circunferencia de radio 15. ¿Cuántas cuerdas de longitud entera pasan por P?. Calcula en cada caso sus longitudes
Instrucciones para participar en el concurso:
- Descarga e imprime el documento en pdf: PROBLEMA5_JUVENIL_3_12_2025
- Realiza la resolución del problema escrito a mano en el documento impreso del punto anterior.
- Escanea en orden ascendente a la numeración de páginas los folios que hayas usado en la resolución del problema. Se guardarán en un único archivo en formato pdf (máx.10MB), nombrado problema-numero-categoría-nombre completo del participante (Ejemplo: problema2AlevinJavierSierraRosa).
- Rellena el formulario para enviar el problema. ( Se solicitan datos del alumnado pero también del representante del menor, que puede ser docente, padre, madre o tutor/a legal).
- Tienes de plazo, si quieres concursar, del 3/12/2025 al 10/12/2025. En el caso que, pasado ese período quieras enviar una resolución, puedes hacerlo, pero ya no entraría en el concurso.
RECUERDA que cuando resuelves un problema tienes que tener en cuenta los datos, anótalos si es relevante la información, realiza las operaciones en orden y explicando las que consideres importantes, y, cómo no, escribe la solución al problema planteado, contestando a la pregunta, generalmente.
Para una información más detallada, echa un vistazo a las bases: Bases del concurso «Retos Olimpiadas»
Si te surgen dudas, contacta con nosotros, te atenderemos gustosamente en Contacta con nosotros.