Problemas propuestos en la Fase Regional de la Olimpiada Matemática 2019 y criterios de corrección.

OLIMPIADA MATEMÁTICA DE EXTREMADURA 2019. FASE AUTONÓMICA. BURGUILLOS DEL CERRO

 

CUBOS CON CARAS NUMERADAS

Antonio elige seis números enteros positivos y distintos, y escribe cada uno en una cara de un cubo. Lanza el cubo tres veces:

– La primera vez salió el cinco en la cara de arriba y la suma de los números de las caras laterales fue 20.

– La segunda vez salió el siete en la cara de arriba y la suma de los números de las caras laterales fue 17.

– La tercera vez salió el cuatro en la cara de arriba y los números de las caras laterales resultaron ser primos.

a. Deduce, de forma razonada, qué número está frente al 4, frente al 5 y frente al 7.

b. Se ha colocado el 7 en el desarrollo plano del cubo, coloca los números que faltan en las restantes caras del cubo.

Nota: Puede haber varias opciones correctas para el desarrollo del cubo, elige solo una.

 

 

RECTÁNGULO DIVIDIDO

El rectángulo ABCD, de área 24 cm², se ha dividido en cinco partes tal y como se muestra en la figura:

Sabiendo que E es el punto medio del segmento DC:

1. ¿Qué relación hay entre las áreas de los triángulos AFE y BFC?
2. ¿Son semejantes los triángulos AFB y EFC? ¿Cuál es la razón entre sus áreas? Justifica tus respuestas.
3. Calcula el área de cada una de las cinco partes en que se ha dividido el rectángulo.

 

EL FRACTAL DE PITÁGORAS

Un fractal es un objeto geométrico de apariencia irregular que está generado a través de una estructura básica que se repite a diferentes escalas dotando a la figura de extraordinaria belleza.

El Árbol de Pitágoras es un fractal inventado en 1942 por Albert Bosman. Su nombre hace honor al célebre matemático griego porque en cada paso aparece un triángulo rectángulo isósceles formado por la unión de tres cuadrados.

Observa la secuencia de construcción:

 

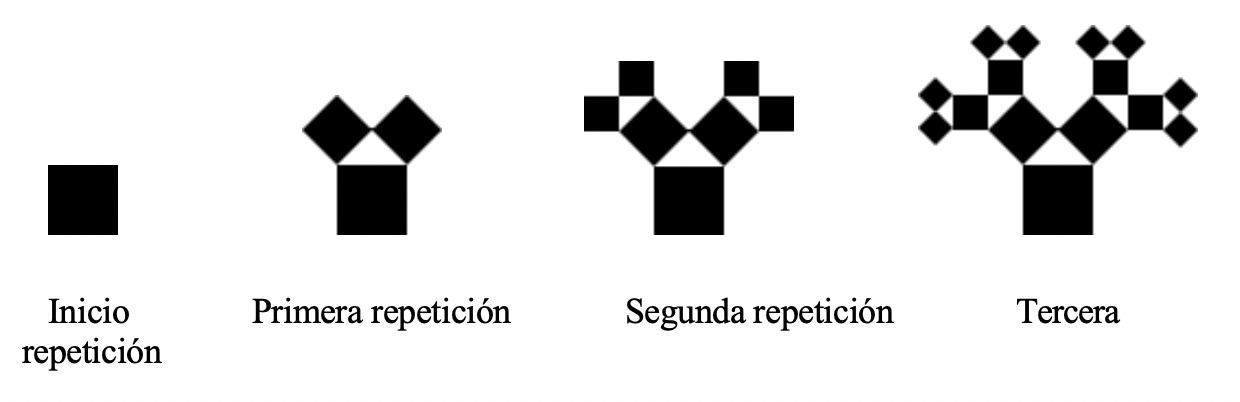
Se quiere construir un Árbol de Pitágoras con cinco repeticiones. Si partimos de un cuadrado de un metro de arista:

1. ¿Cuántos cuadrados aparecerán en este fractal? ¿y cuántos triángulos?
2. Calcula la longitud de los catetos de los triángulos que se añaden en cada repetición.

Ayuda: Se recomienda no utilizar las expresiones decimales de las raíces.

c. Si en lugar de construir el Árbol de Pitágoras con cinco repeticiones queremos hacerlo con n (siendo n un número natural), ¿podrías indicar cuántos cuadrados y triángulos tendría la figura? ¿cuál será la longitud de los catetos de los triángulos más pequeños?

 

POTENCIAS DE DOS

1. Indica en qué cifra terminan los números 2⁵, 2¹⁸, 2¹⁰⁰ y 2²⁰¹⁹.
2. Calcula la cifra de las unidades del número 2ⁿ según los valores del exponente n, siendo n un número natural.
3. Se considera la suma 2+2²+2³+2⁴+…+2ⁿ donde n es un número natural. ¿Para qué valores de n esta suma termina en cero?

Criterios de correción