Problema 2: Concurso «Retos olimpiadas » Alevín (6º EP)
Soluciones:
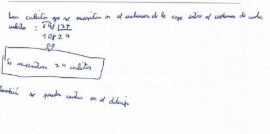
Hemos recibido tres resoluciones del problema 2 para la categoría alevín, ¡animaros a seguir participando!
A continuación os facilitamos la solución oficial del problema 2:
Sobre el DNI y el NIF
El Documento Nacional de Identidad (DNI) consta de un número de 8 cifras seguido de una letra (el NIF o Número de Identificación Fiscal), que permite detectar si el número está correctamente escrito.
Para saber la letra, se divide el número del DNI entre 23 y como hay 23 restos posibles, se hace corresponder cada resto con una letra escrita en mayúscula del alfabeto, (todas excepto I, Ñ, O, U) según la siguiente tabla:
| Resto | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Letra | T | R | W | A | G | M | Y | F | P | D | X |
| Resto | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| Letra | B | N | J | Z | S | Q | V | H | L | C | K | E |
a) ¿Cuál es el primer número anterior al de Lucía que tiene asignada la letra Z?
b) Los DNI de dos amigos Antonio y Lucía son: 06 940 760 y 23 768 976 ¿cuáles son las letras correspondientes a esos carnés?
c) ¿Cuál es el primer número anterior al de Antonio con su misma letra?
d) ¿Cuál es el primer número posterior al de Lucía con su misma letra?
e) ¿Cuál es el primer número posterior al de Antonio que tiene asignada la letra Z?
Solución oficial:
a) El de Antonio tiene asignada la letra G y el de Lucía la V porque al dividir sus DNI entre 23 se obtienen restos 4 y 17 respectivamente.
b) Si al dividir dos números entre 23 dan el mismo resto, tendrán la misma letra. Si restamos al DNI de Antonio 23, el número resultante es el anterior con el mismo resto, es decir: 06 940 760 – 23 = 06 940 737
c) De forma similar para que sea posterior al de Lucía con la misma letra debe ser: 23 768 976 + 23 = 23 768 999
d) Para que tenga asignada la letra Z, el resto de dividir entre 23 debe ser 14. Como el resto del de Antonio es 4, para que sea 14 debe ocurrir: 06 940 760 + 10 = 06 940 770
e) Como el resto del de Lucía es 17 y queremos que sea 14 para que la letra sea la Z, debe ser: 23 768 976 – 3 = 23 768 973
La resolución elegida como ganadora del problema 2 ha sido la realizada por Darío M. D. del CEIP Sebastián Martín (Montehermoso) ¡¡ Enhorabuena !!



Enunciado:
22-octubre-2025
A continuación puedes ver el enunciado del problema 2 para el concurso «Retos Olimpiadas», en la categoría Alevín, 6º EP.
¡¡ Anímate a participar !! Para ello sigue las instrucciones que encontrarás tras el enunciado.
Enunciado problema 2:
Sobre el DNI y el NIF
El Documento Nacional de Identidad (DNI) consta de un número de 8 cifras seguido de una letra (el NIF o Número de Identificación Fiscal), que permite detectar si el número está correctamente escrito.
Para saber la letra, se divide el número del DNI entre 23 y como hay 23 restos posibles, se hace corresponder cada resto con una letra escrita en mayúscula del alfabeto, (todas excepto I, Ñ, O, U) según la siguiente tabla:
| Resto | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Letra | T | R | W | A | G | M | Y | F | P | D | X |
| Resto | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| Letra | B | N | J | Z | S | Q | V | H | L | C | K | E |
a) ¿Cuál es el primer número anterior al de Lucía que tiene asignada la letra Z?
b) Los DNI de dos amigos Antonio y Lucía son: 06 940 760 y 23 768 976 ¿cuáles son las letras correspondientes a esos carnés?
c) ¿Cuál es el primer número anterior al de Antonio con su misma letra?
d) ¿Cuál es el primer número posterior al de Lucía con su misma letra?
e) ¿Cuál es el primer número posterior al de Antonio que tiene asignada la letra Z?
Instrucciones para participar en el concurso:
- Descarga e imprime el documento en pdf: PROBLEMA2_ALEVÍN_22_10_2025
- Realiza la resolución del problema escrito a mano en el documento impreso del punto anterior.
- Escanea en orden ascendente a la numeración de páginas los folios que hayas usado en la resolución del problema. Se guardarán en un único archivo en formato pdf (máx.10MB), nombrado problema-numero-categoría-nombre completo del participante (Ejemplo: problema2AlevinJavierSierraRosa).
- Rellena el formulario para enviar el problema. ( Se solicitan datos del alumnado pero también del representante del menor, que puede ser docente, padre, madre o tutor/a legal).
- Tienes de plazo, si quieres concursar, del 22/10/2025 al 29/10/2025. En el caso que, pasado ese período quieras enviar una resolución, puedes hacerlo, pero ya no entraría en el concurso.
RECUERDA que cuando resuelves un problema tienes que tener en cuenta los datos, anótalos si es relevante la información, realiza las operaciones en orden y explicando las que consideres importantes, y, cómo no, escribe la solución al problema planteado, contestando a la pregunta, generalmente.
Para una información más detallada, echa un vistazo a las bases: Bases del concurso «Retos Olimpiadas»
Si te surgen dudas, contacta con nosotros, te atenderemos gustosamente en Contacta con nosotros.