Skip to main content

Autor: javierc

Enlace al vídeo explicativo. Espiral Áurea

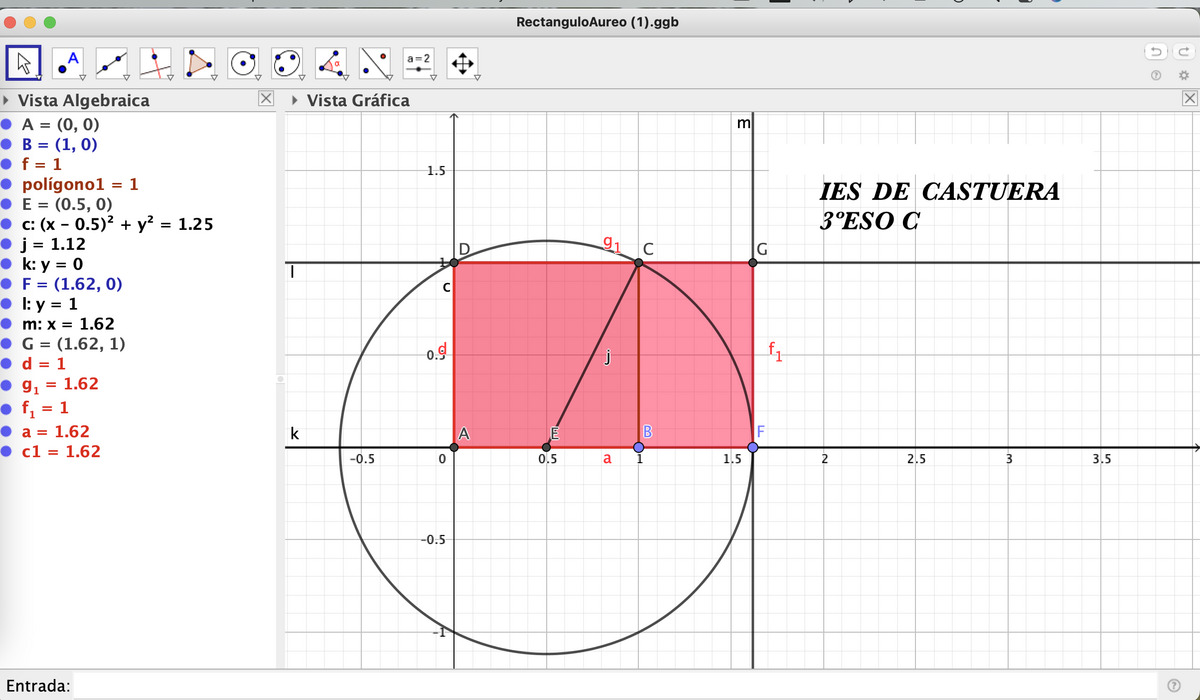
Espiral áurea en el IES Castuera

Escrito por javierc en . Publicado en Instituto GeoGebra.

Somos Mª Soledad Sánchez y Lola Segura, profesoras del IES Castuera.
 
Hemos realizado esta actividad con el alumnado de 3º ESO. El proyecto de este trimestre trata sobre la proporción áurea así que a lo largo del mismo realizamos contribuciones al proyecto central. 
 
En este caso hemos utilizado GeoGebra para construir un rectángulo áureo y una espiral áurea. Para esta sesión nos trasladamos al Aula de Informática. Nuestro alumnado está familiarizado con las herramientas de GeoGebra puesto que han trabajado con el programa desde 1ºESO, por lo que nos centramos en explicarles la construcción de un rectángulo áureo a través de un vídeo explicativo:
 
 
Tras la visualización del mismo, el alumnado se dispuso a realizar individualmente la construcción así como a personalizarla (colores, mostrar/ocultar elementos,…)  Usamos la versión de GeoGebra online. El alumnado se registró usando sus cuentas de educarex.
Todos los alumnos y alumnas realizaron las construcciones pedidas, la mayoría incluso mejoró estéticamente la construcción propuesta en el vídeo. 
Adjuntamos un par de imágenes del resultado.
iescastuera espiral aurea
 
 
iescastuera rectangulo aureo
 
La valoración que hacemos de la experiencia es muy positiva. El uso de GeoGebra les ayudó a definir un protocolo de construcción y seguirlo. El alumnado se mostró muy motivado durante la sesión.
mediciones

Medida Histórica de la distancia Tierra-Sol

Escrito por javierc en . Publicado en Instituto GeoGebra.

En este artículo, nuestros compañeros Fedra Gregorio Díaz y Jesús Manuel Carballar Álvarez, del IES El Pomar de Jerez de los Caballeros, nos cuentan los detalles del proyecto Aristarco (Proyecto de Innovación Educativa por la Junta de Extremadura), en el que utilizaron GeoGebra para calcular el ángulo formado entre la Tierra, la Luna y el Sol y, posteriormente, dar una aproximación de la distancia de la Tierra al Sol.

El proyecto ha sido creado por Jesús Manuel Carballar Álvarez, jefe del departamento de Matemáticas del IES El Pomar. Para llevarlo a cabo, se han coordinado 3 centros educativos, efectuando la reproducción de la medida de la distancia de la Tierra al Sol realizada por el matemático y astrónomo griego Aristarco de Samos hace más de XXII siglos. Los centros educativos que han participado en la obtención de esta medida han sido el IES El Pomar (Jerez de los Caballeros, Badajoz), el IES Ramón Carande (Jerez de los Caballeros, Badajoz) y el IES La Orotava – Manuel González Pérez (Tenerife).

Continuar leyendo

Coordenadas cilíndricas en GeoGebra

Escrito por javierc en . Publicado en Instituto GeoGebra.

Por ahora, GeoGebra no permite introducir directamente coordenadas cilíndricas. Pero como son combinación de las coordenadas polares y las cartesianas, podemos escribirlas como suma de estas dos. Para ello, bastará con escribir la parte en coordenadas polares (radio;ángulo), más la parte cartesiana como (0,0,altura). No olvidemos usar el «;» para separar el radio del ángulo, que es la forma de indicar a GeoGebra que estamos utilizando coordenadas polares. La expresión sería

CoordenadaCilindrica= (radio; ángulo)+(0,0,altura)

Por ejemplo, para crear un cilindro de radio 8, entre -10 y 10:

Superficie((8; t) + (0, 0, s), t, 0, 2π, s, -10, 10)

Igualmente, podemos crear otras figuras como las mostradas a continuación en este applet, con los siguientes comandos

Superficie1 = Superficie((5 + 2cos(s); t) + (0, 0, s), t, 0, 2π, s, -6 π, 6π) Superficie2 = Superficie((s + 2cos(s); t) + (0, 0, s), t, 0, 2π, s, -6 π, 6π)

Enlace en GeoGebra: https://www.geogebra.org/m/ekqxctrt

autoevaluables1

Actividades autoevaluables que han venido para quedarse

Escrito por javierc en . Publicado en Instituto GeoGebra.

Las actividades autoevaluables de GeoGebra han venido para quedarse y la razón es que, si están bien estructuradas y pensadas, facilitan la autonomía en el aprendizaje del alumnado, sobre todo en los procedimientos más mecánicos.

Estas actividades tienen dos características que las hacen muy potentes:

  • el trabajo con números aleatorios que hace infinita la lista de propuestas para cada alumno o alumna y, por otro lado,
  • el botón que te permite corregir y saber si lo has resuelto bien. Si, además, te indica el camino completo para llegar a la resolución o te da la opción, a través de pistas, para ir pautando el proceso, conseguimos que se fomente aún más el autoaprendizaje.

Continuar leyendo