Cuadrados antimágicos y otros

Mayo de 2025

Son conocidos los cuadrados mágicos que son distribuciones de los “n² ” primeros números en cuadrados de tal manera que la suma de los números de una fila, una columna o una diagonal siempre sea la misma.

• Actividad: Con los números del 1 al 9, ¿cuánto tendrían que sumar los números de una fila, columna y diagonal de un cuadrado mágico de orden tres?
• Actividad: Con los números del 1 al 9 podemos construir ocho cuadrados mágicos diferentes, ¿podrías reproducirlos?
• Actividad: Construye un cuadrado mágico con los números del 1 al 16, ¿cuánto tendrían que sumar los números de una fila, columna y diagonal de un cuadrado mágico de orden cuatro?

Algunos ejemplos:

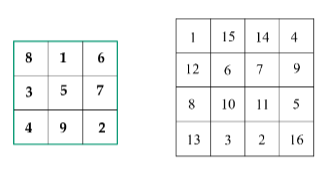
Podríamos seguir estudiando cuadrados mágicos de orden superior y estudiar sus propiedades e incluso, su estructura algebraica. Hay mucha literatura sobre ello y te animo a que la busques y la trabajes.

Cuadrados antimágicos

En contraposición a los cuadrados mágicos podríamos pensar si existen cuadrados numéricos en los que la suma de las filas, columnas y diagonales fueran siempre diferentes.
Los cuadrados que cumplen con esa condición se les llama cuadrados antimágicos, y son más escasos que los mágicos.

• Actividad: Con los números del 1 al 9, ¿Podrías encontrar un cuadrado antimágico de orden tres?

No te desanimes, y prueba a ver si encuentras un cuadrado antimágico de orden cuatro.

• Actividad: Con los números del 1 al 16, encuentra un cuadrado antimágico de orden cuatro.

Aquí es posible que hayas tenido más suerte o acierto. Si no lo has encontrado debes saber que existe al menos uno.

Otros cuadrados misteriosos

En el libro de José M. Albaiges Olivartt, “¿Se atreve Usted con ellos? 10 apasionantes problemas”. De la editorial Marcombo, aparece un cuadrado misterioso que reproduzco:

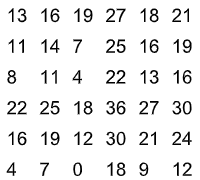
• Actividad: ¿Cuántos suman los números de las diagonales?
• Actividad: Escoge un número del cuadrado y tacha su fila y su columna. Coge otro número de los restantes no tachados y haz la misma operación. Así, mientras queden números libres. Suma los seis números que hayas escogido.
• Actividad: Repite la acción anterior con otros números y analiza el resultado.