Sigue con los problemas….pero de los tuyos. Jugando con las matemáticas. Enseñar / aprender a resolver problemas.
Inventando fórmulas
Nos empeñamos demasiadas veces en resolver los problemas de cálculo de superficies o volúmenes empleando una determinada fórmula, aun sabiendo que pueden resolverse de otras maneras diferentes (composición y descomposición de figuras, aproximación por exceso y por defecto, fórmula e Herón, etc.), que pueden resultar más sencillas y útiles. Los estudiantes se quejan de tener que aprenderse las fórmulas de memorias por lo que nos ha parecido interesante retomar este juego con ellas.
Descubrir fórmulas es algo que les llama la atención a los nuevos resolutores y flipan en colores si a la fórmula le ponemos el nombre de quién ha sido capaz de reconocerla. Además, proporciona información que nos será útil en numerosas ocasiones.
- Calcular el área de un triángulo rectángulo.
El recuerdo y la obligación implícita que asumen de tener que utilizar la fórmula dada le lleva en ocasiones o no buscar o pensar procedimientos más fáciles y cuando se los mostramos nos podemos llevar la sorpresa de que algunos nos diga: “Yo lo había pensado, pero …”
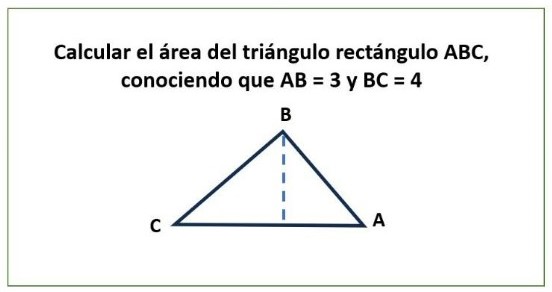
Lo usual es que los estudiantes de secundaria traten de resolver el problema calculando la hipotenusa (CA) y dividiéndola en dos partes y aplicando el teorema de Pitágoras, cuando hay un procedimiento más inmediato y fácil jugamos con las figuras y las fórmulas.
Así, por ejemplo, recuerdo una ocasión en la que una alumna me dijo: “Profe, puedo calcular el área de un triángulo rectángulo multiplicando los catetos y dividiendo el resultado por dos, Atr = (C1 x C2)/2.”
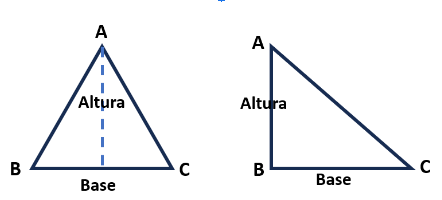
Un simple giro en el folio que había en su mesa con los triángulos dibujados le hizo observar que el triángulo rectángulo dibujado un cateto era una base y el otro la altura correspondiente. A partir, de esa observación construyó su nueva fórmula.
Aproveché esta situación para generar nuevos problemas:
- “Comprueba con diferentes ejemplos que la fórmula propuesta por tu compañera funciona.”
Obviamente, comprobar esta afirmación puede hacerse de diferentes maneras según el nivel educativo. En secundaria podría hacerse siguiendo el procedimiento del cálculo de la hipotenusa y la altura utilizando ecuaciones, y en primaria podremos utilizar un procedimiento mas visual y sencillo a partir de la descomposición de un rectángulo en dos triángulos rectángulos.
La figura nos muestra que para calcular el área del triángulo ABC multiplicaremos el valor de los catetos y lo dividiremos por dos. Y esto vale siempre para los triángulos rectángulos ya que si elegimos un cateto como base el otro cumple con la definición de altura.
En cualquier caso, es bueno recordar la posición relativa de las alturas en los triángulos.
2. Calcular el área de un cuadrado.
Otro alumno me dijo, en otra ocasión, que “el área de un cuadrado se calcula multiplicando la diagonal por ella misma y dividiendo el resultado por dos. Es decir, A = dxd/2.”
Rápidamente, otros alumnos indicaron que se había equivocado porque que eso era la fórmula para calcular el área de los rombos. Yo dejé que discutirán entre ellos, pero la situación me llevó a plantear las siguientes cuestiones:
- “Comprueba con diferentes ejemplos que esa fórmula (d2/2) funciona para calcular el área de un cuadrado”.
- “¿Sabrías justificar que la fórmula del cálculo de área de un rombo puede aplicarse a los cuadrados en base a las definiciones de ambos cuadriláteros?”
- “Dado que las dos diagonales del cuadrado son iguales, ¿sabrías justificar que la fórmula d2/2 puede aplicarse a los cuadrados a partir de la expresión A = l2 para el cálculo de área de cuadrado?”
4. “Busca las relaciones de inclusión de las definiciones de cuadrado, rectángulo, rombo y romboides.
Para profundizar sobre esta cuestión podemos recurrir al libro “Aprender a enseñar Geometría en primaria” que está disponible en la dirección:
https://dehesa.unex.es/bitstream/10662/5243/1/978-84-606-9500-4.pdf
3. El área del circulo y la longitud de la circunferencia.
Un tercer caso muy sencillo se refiere a la fórmula para calcular la longitud de la circunferencia multiplicando el valor del diámetro por pi (π). En normal que si le proponemos a los estudiantes calcular la longitud de la circunferencia dando el valor del diámetro lo primero que hagan sea calcular el radio y aplicar la fórmula L = 2π r. Es consecuencia de la metodología empleada en el aula.
Sin embargo, el cálculo debería ser inmediato si jugamos con las fórmulas.
- “¿Sabrías justificar que la fórmula “l = d x π” es válida para calcular la longitud de la circunferencia?”
- “Si conocemos el diámetro de un círculo podríamos utilizar la fórmula πd2/4 para calcular su área?”
- “Si dividimos la longitud de la circunferencia por el diámetro que obtendremos?”
- “Si dividimos el área del círculo por π, ¿qué obtendremos?”
Lorenzo J. Blanco Nieto
@lorenzojblanco
https://maniasmatematicas.blogspot.com