Problema 6: Concurso «Retos olimpiadas » Juvenil (4º ESO)
Soluciones:
Hemos recibidos 6 resoluciones del problema 6 en la categoría juvenil, gracias por participar.
A continuación os facilitamos la solución oficial del problema 6:
CUADRADO DIVIDIDO
Este cuadrado de 10 m de lado se ha dividido en 9 partes: 4 triángulos iguales, 4 trapecios iguales y un cuadrado. Calcula el área y el perímetro de cada una de esas tres partes.
Solución
Hay 4 son trapecios rectángulos, 4 triángulos rectángulos y un cuadrado. Añadiendo cada uno de los 4 triángulos a los trapecios por la parte externa, se forma una cruz con cinco cuadrados iguales.
Si el área del cuadrado es 100 m2, el área de cada cuadrado es la quinta parte, es decir 20 m2
La franja central es un paralelogramo que está formado por el cuadrado y dos trapecios y su área es 10 . 5 = 50 m2. Como el cuadrado mide 20 m2, los dos trapecios medirán:
50 – 20 = 30 m2 y cada uno de ellos 15 m2
El triángulo de la parte izquierda o derecha, es ¼ del cuadrado es decir 25 m2 y está formado por dos triángulos pequeños y un trapecio, luego los dos triángulos miden: 25 – 15 = 10 m2 y cada triángulo mide 5 m2
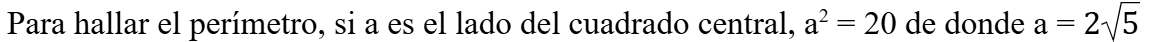
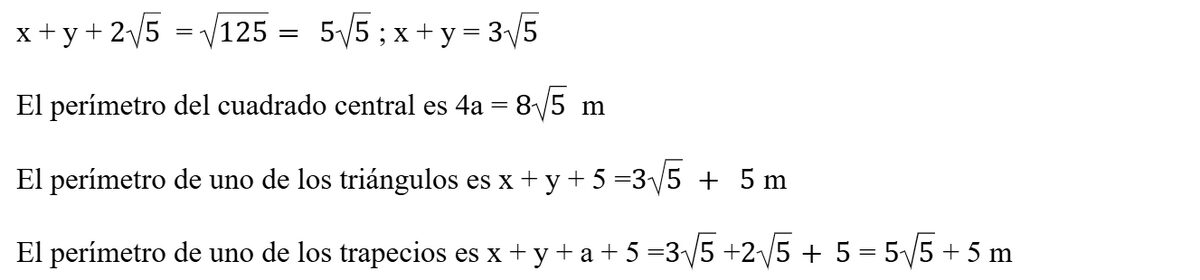
Otra Forma
Sin la idea feliz anterior, se puede hacer:
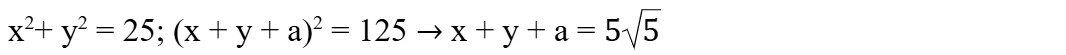
Las bases del trapecio son x e y, la altura es a, entonces:
a2 + (y-x)2 = 25 y como x2+ y2 = 25 se sigue que a2 – 2xy = 0 de donde a2 = 2xy
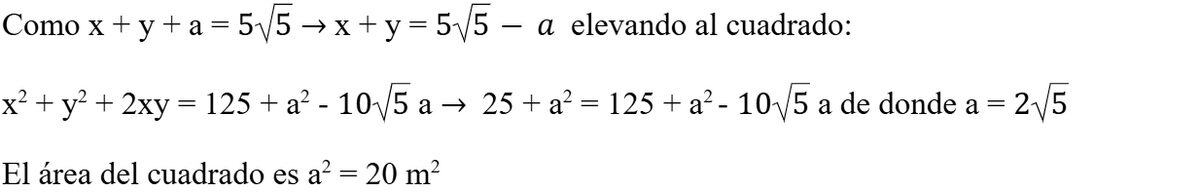
Las resoluciones recibidas han sido variadas, con aciertos en muchas de ellas, se ha elegido aquella que estaba correcta y que mejor ha justificado los pasos que ha seguido para resolver el problema 6. IMPORTANTE: Os recordamos la conveniencia de utilizar números irracionales mejor que decimales por la elegancia y mayor exactitud.
La resolución elegida como ganadora del problema 6 ha sido la realizada por Emilio Bravo Salgado del Salesianos Ramón Izquierdo Badajoz. ¡¡ Enhorabuena !!




Enunciado:
5-marzo-2025
A continuación puedes ver el enunciado del problema 6 para el concurso «Retos Olimpiadas», en la categoría Juvenil (4º ESO).
¡¡ Anímate a participar !! Para ello sigue las instrucciones que encontrarás tras el enunciado.
Enunciado problema 6:
CUADRADO DIVIDIDO
Este cuadrado de 10 m de lado se ha dividido en 9 partes: 4 triángulos iguales, 4 trapecios iguales y un cuadrado. Calcula el área y el perímetro de cada una de esas tres partes.
Instrucciones para participar en el concurso:
- Descarga e imprime el documento en pdf: PROBLEMA6_JUVENIL_05_03_2025
- Realiza la resolución del problema escrito a mano en el documento impreso del punto anterior.
- Escanea en orden ascendente a la numeración de páginas los folios que hayas usado en la resolución del problema. Se guardarán en un único archivo en formato pdf (máx.10MB), nombrado problema-numero-categoria-nombre completo del participante (Ejemplo: problema2AlevinJavierSierraRosa).
- Rellena el formulario para enviar el problema. ( Se solicitan datos del alumnado pero también del representante del menor, que puede ser docente, padre, madre o tutor/a legal).
- Tienes de plazo, si quieres concursar, del 5/03/2025 al 12/03/2025. En el caso que, pasado ese período quieras enviar una resolución, puedes hacerlo, pero ya no entraría en el concurso.
RECUERDA que cuando resuelves un problema tienes que tener en cuenta los datos, anótalos si es relevante la información, realiza las operaciones en orden y explicando las que consideres importantes, y, cómo no, escribe la solución al problema planteado, contestando a la pregunta, generalmente.
Para una información más detallada, echa un vistazo a las bases: Bases del concurso «Retos Olimpiadas»
Si te surgen dudas, contacta con nosotros, te atenderemos gustosamente en Contacta con nosotros.