Skip to main content

Traducir una situación concreta al lenguaje algebraico. (II)

Escrito por Administrator en . Publicado en Jugando con las matemáticas, Llévatelo a tu aula, Portada.

Marzo de 2025

En la actividad anterior (actividad del mes de febrero 2025) señalábamos las dificultades del paso de una situación concreta a una expresión algebraica que la represente. Terminábamos la entrada con un problema que reproducimos de nuevo:

“Escribe una ecuación usando las variables Q y M para representar la siguiente afirmación: En un restaurante, por cuatro personas que piden tarta de queso (Q), hay cinco que la piden de manzana (M)” (Lochead y Mestre, 1988, 127).

Supongo que los habréis propuesto y analizado en vuestras aulas.

En este caso, la típica respuesta es: 4 Q = 5 M, a pesar de que los resolutores puedan comprender y representar la relación numérica entre el número de comensales en cada caso. Es decir, a pesar de que los resolutores puedan asumir la comprensión cualitativa y cuantitativa.

El paso de la comprensión cuantitativa requiere de una representación adecuada ya que la traducción a la expresión algebraica es visualizar la igualdad de la multiplicación en cruz. No es fácil el paso de los números a las letras, que nos dicen.

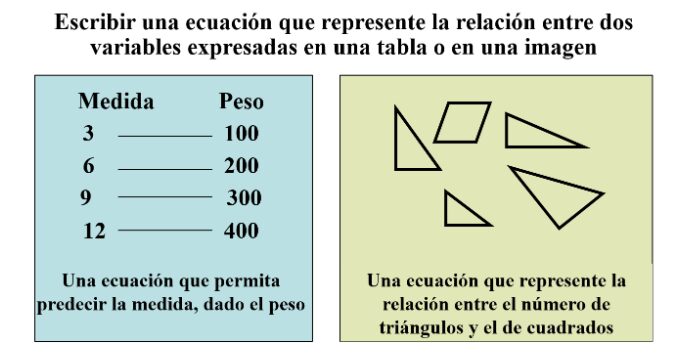
Os dejo otros problemas similares.
“Fui a la tienda y compré el mismo número de libros que de discos. Los libros me costaron dos euros cada uno y los discos seis euros cada uno. Gasté en total 40 euros.”

  • Lochhead, J; Mestre, JP. From words to algebra: mending misconcepcions. En Coxford, AF; Shulte, AP (Eds.): The ideas of Algegra, K-12 (1988 y Yearbook). Reston, VA: NCTM, 1988 pp. 127-135.
  • Blanco, L.J. (2025). La resolución de problemas de matemáticas en la formación inicial de profesores de primaria. Servicio de publicaciones de la UEX.

Lorenzo J. Blanco Nieto
@lorenzojblanco
https://maniasmatematicas.blogspot.com